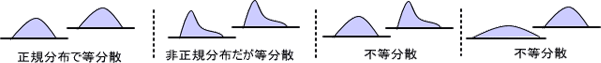SPSS使い方|中央値の出し方やt検定のやり方など【備忘録】

私的備忘録レベルで、SPSSの使い方を記事にします。
「SPSSの使い方が知りたい」
「t検定がやりたい」
「MWT-U検定がやりたい」
「標準偏差が出したい」
「中央値が出したい」
「パーセントタイルが出したい」
「ロジスティック回帰分析がやりたい」
上記を解決すべく、SPSSの使い方(操作方法)を解説。
そもそも、何検定を使うか
検定には種類がある
個人的によく使うのは以下
- 対応のないt検定
- MWT-U(マンホイットニーのU検定)
- カイ二乗(カイジジョウ)検定
- ログランク検定(カプランマイヤー法)
です。
t検定ついて
t検定とは
t検定は「2つの間の平均値に有意な差があるか」をみる検定。
例えば、2つのグループの「年齢の差」とか「算数の点数の差」とか。
t検定の種類(対応のある、ない)
そもそもt検定は、
- 対応のあるt検定
- 対応のないt検定
の2つに分かれる。
- 対応のあるt検定とは→1つのグループの中での前後を調べる
- 対応のないt検定とは→2つのグループの差を調べる
<対応のあるt検定の例>
「5年2組の生徒に、とある問題集をさせてみて、やる前とやった後で、算数のテストに点数に差があったのかどうか」を調べたいなら、対応のあるt検定。
<対応のないt検定の例>
「5年1組と5年2組の算数の授業のやり方を違う方式でやってるのだけど、それぞれの算数のテストの平均点に差があるのかどうか」を調べたいなら、対応のないt検定。
対応のないt検定のやり方
SPSS内の操作方法
分析→平均の比較→独立したサンプルのt検定
操作方法はこのサイトが分かりやすい>t検定|SPSSの使い方
t検定は、母群間が「正規分布」で「等分散」していなければいけない。
正規分布するかどうか迷ったら、ノンパラメトリック検定(マンホイットニーのU検定)を選択する。
正規分布に従うか迷う場合はノンパラメトリック解析を選択しましょう。
なぜなら有意差が出にくいノンパラ解析で、「有意差あり」なら「確実に有意差がある」からです。
-中略-
しかし、MWUで「有意差なし」でも「有意差なし」でもt-testで有意差が検出されることがあるので、そういう場合は、母集団の正規分布の検討が必要です。
等分散しているかどうか検討は「F検定」を行う必要がある。
F検定のやり方と統計量F(F値)
F検定によって求めた統計量F(F値)によって、等分散するかどうかを判定する。
・仮説の設定
帰無仮説(H0):「2群間の分散に差がない(等分散である)」と仮定する。
対立仮説(H1):「2群間の分散に差がある(等分散でない)」と仮定する。-中略-
・判定
1≦F≦Fαのとき、P>0.05となる→帰無仮説を棄却できない→等分散である。
F>Fαのとき、P<0.05となる→帰無仮説を棄却する→不等分散である。
FαはF分布表で確認する。
F値は、比較したいA群とB軍の不偏分散の割り算で求める。
このとき、分子の方が大きい数値になるようにする。
F値がF分布表の値よりも大きい場合→「帰無仮説(等分散である)」を「棄却する」ので、要は2群は「等分散していない」という事になる。
F値がF分布表の値よりも小さい場合→「帰無仮説(等分散である)」を「採択する」ので、要は2群は「等分散している」ということになる。
中央値について(1つの群の中央値の出し方)
1つの群の中央値は、順番に並べた時の真ん中の順位の値となる。
20、50、20、10、30、10、30、20、10というデータなら、
まず10、10、10、20、20、20、30、30、50と並び変える。
そして、真ん中の20が中央値である。
奇数のデータは真ん中があるが、偶数のデータなら、真ん中2つを足して2で割った値が中央値。
MWT-U検定のやり方(P値、中央値、パーセントタイル)
日付や係数など、平均値に“ばらつき”がある(正規分布しない)集団の検定は「ノンパラメトリック検定」を行い「中央値」と「パーセントタイル」を出す。
MWT-U検定|P値の出し方
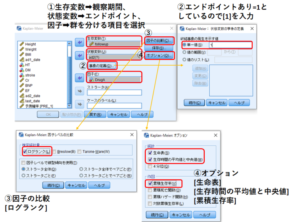
P値の出し方:分析→ノンパラメトリック検定→過去のダイアログ→2個の独立サンプルの検定
「検定変数リスト」に検定した項目を選ぶ
「グループ化変数」に0,1で因子を選ぶ
MWT-U検定|中央値、パーセントタイルの出し方
MWT-U検定の場合、中央値とパーセントタイルも必要。
中央値、パーセントタイルの出し方:分析→記述統計→探索的
カイ二乗(カイジジョウ)検定のやり方
分析→記述統計→クロス集計表
「行」と「列」を選択。
統計量を「カイ二乗検定」にチェックを入れる。
>クロス集計|SPSSの使い方 (kokugakuin.ac.jp)
Log-Lank(ログランク)検定のやり方
Log-Lank(ログランク)は、イベント発生の検定を行うときに使う。
カプランマイヤー曲線というもので表される。
何に何検定をあてはめるのか
2群間を平均値などで比較する場合
- 正規分布する場合→パラメトリック検討(t検定など)
- 正規分布しない場合→ノンパラメトリック検定(MWU検定など)
- 同じ母集団の時間別での比較→対応のあるt検定
- 違う母集団の比較→対応のないt検定
原因の有無で比較する場合
- 性別(0,1)で分けたり、疾患の有無(0,1)で分けた検定→解二乗検定
イベント発生などを比較する場合
- 生存曲線→Log-Lank検定
原因の検索を探す場合(因子検討)
- 従属変数に時間的要素がある場合→Cox回帰分析(比例ハザード分析)
- 従属変数に時間的要素がなく、0,1(有無)で表される場合→ロジスティック回帰分析
- 従属変数に時間的要素がなく、量的なデータの場合→重回帰分析
そもそも従属変数とか独立変数って?
従属変数は、結果の方。
独立変数は、原因となるものの方。
独立変数(例えば「年齢」「残業時間」)によって、従属変数(例えば「年収」)が高いか低いか。
独立変数(例えば「塾に通っているか」「学習時間が長いか短いか」「自分の勉強部屋があるかないか」)によって、従属変数(例えば「テストの点数」)が良いのか悪いのか。
多重共線性とは
多重共線性とは、原因となる項目が似ていて、関係性が強すぎるもののこと。
例えば、年収を比べる場合に「年齢」と「経験年数」は関係性が強いし、テストの点数を比べる場合に、「塾での学習時間」と「学校以外での学習時間」は関係性が強いので、原因の項目に投入するときに注意する必要がある。
ロジスティック回帰分析のやり方
原因の検索は「ロジスティック回帰分析」でできます。
分析→回帰→二項ロジスティック
まずは原因と考えられる項目すべてを「ブロック」の項目に追加します。
そして「強制投入法」で解析します。
参考サイト>SPSSでロジスティック回帰分析 | みんなの疫学統計教室
すると「どれが原因なのか」が分かります。
ここまでが「単変量解析」です。
ロジスティック回帰分析の単変量解析
単変量解析では、その事象が起こる原因がすべて検出されます。
つまり、2つも3つも出てきてしまいます。
例えば「テストの点数が悪い理由」を調べたとき、「自宅での学習時間」とか「ゲームをしている時間」とか「塾に通っているかどうか」とかです。
でも、「ゲームをしていること」がよくないのか「ゲームをしているから、自宅での学習時間が短いのか」は、ハッキリしません。
そこで、「本当に一番影響している原因は何か」を探るには「多変量解析」が必要となります。
ロジスティック回帰分析の多変量解析
多変量解析は「本当に一番影響を与えている原因は何なのか」を探すことができます。
分析→回帰→二項ロジスティック
でロジスティック回帰分析を選択するまでは、単変量解析と同じです。
そこから「単変量解析で、有意差が出た項目だけをブロックのところに入れて、検定をかける」ことで、多変量解析ができます。
このとき「方法」のところを、「強制投入法」ではなく「尤度比」を選択しましょう。